Binomial Option Pricing -mallin ymmärtäminen

Osakkeiden hintojen määrittäminen

Kaikkien vaihdettavissa olevien varojen tarkan hinnoittelun sopiminen on haastavaa - siksi osakekurssit muuttuvat jatkuvasti. Todellisuudessa yritykset tuskin muuttavat arvostuksia päivittäin, mutta niiden osakekurssit ja arvostukset muuttuvat lähes joka sekunti. Tämä vaikeus päästä yksimielisyyteen kaupankäynnin kohteena olevan omaisuuden oikeasta hinnoittelusta johtaa lyhytikäiseen arbitraasi mahdollisuudet.

Mutta monet onnistuneet sijoitukset johtuvat yksinkertaisesta kysymyksestä nykypäivän arvostamisesta-mikä on oikea nykyinen hinta tänään odotetun tuoton vuoksi?

Avain takeaways

Binominen optioiden hinnoittelumalli arvostaa vaihtoehtoja iteratiivisella lähestymistavalla, joka käyttää useita kausia amerikkalaisten optioiden arvostamiseen.
Mallilla on kaksi mahdollista tulosta jokaisella iteroinnilla - siirtyminen ylös tai alas, joka seuraa binomipuuta.
Malli on intuitiivinen ja sitä käytetään käytännössä useammin kuin tunnettua Black-Scholes-mallia.

instagram viewer

Binomiovaihtoehtojen arviointi

Kilpailukykyisillä markkinoilla välttääkseen arbitraasimahdollisuuksia, omaisuutta samanlaisilla voittorakenteilla on oltava sama hinta. Vaihtoehtojen arvostus on ollut haastava tehtävä ja hinnoitteluvaihtoehdot johtavat arbitraasimahdollisuuksiin. Musta-Scholes on edelleen yksi suosituimmista hinnoittelumalleista vaihtoehtoja mutta sillä on rajoituksia.

The binomioption hinnoittelu malli on toinen suosittu menetelmä hinnoitteluvaihtoehdot.

Esimerkkejä

Oletetaan, että on olemassa a soittovaihtoehto tietyssä osakkeessa, jossa on virta markkinahinta 100 dollaria. The rahalla (ATM) -vaihtoehdossa on lakkohinta 100 dollaria, ja niiden voimassaoloaika päättyy vuoden. On olemassa kaksi kauppiaata, Peter ja Paula, jotka molemmat ovat yhtä mieltä siitä, että osakekurssi joko nousee 110 dollariin tai laskee 90 dollariin vuodessa.

He sopivat odotetusta hintatasosta tietyn vuoden aikana, mutta ovat eri mieltä ylös- tai alas -liikkeen todennäköisyydestä. Peter uskoo, että osakkeen hinnan todennäköisyys 110 dollariin on 60%, kun taas Paula uskoo sen olevan 40%.

Kuka tämän perusteella olisi valmis maksamaan enemmän hintaa ostovaihtoehdosta? Mahdollisesti Peter, koska hän odottaa suurta todennäköisyyttä ylöspäin.

Binomiasetusten laskelmat

Kaksi omaisuutta, joista arvostus riippuu, ovat osto -optio ja kohde -etuutena oleva osake. Osallistujien kesken on sovittu, että taustalla oleva osakekurssi voi siirtyä nykyisestä 100 dollarista joko 110 dollariin tai 90 dollariin vuodessa, eikä muita hintojen siirtoja ole mahdollista.

Jos arbitraasittomassa maailmassa joudut luomaan salkun, joka koostuu näistä kahdesta omaisuudesta, osto-optiosta ja taustalla olevasta osakkeesta, niin, että riippumatta siitä, mihin kohdehinta menee - 110 dollaria tai 90 dollaria - salkun nettotuotto on aina sama. Oletetaan, että ostat kohde -etuutena olevia d -osakkeita ja lyhyitä osto -optioita tämän salkun luomiseksi.

Jos hinta nousee 110 dollariin, osakkeiden arvo on 110 dollaria*d ja menetät 10 dollaria lyhyt puhelu loppuratkaisu. Salkun nettoarvo on (110d - 10).

Jos hinta laskee 90 dollariin, osakkeiden arvo on 90 dollaria*d, ja optio vanhenee arvottomana. Salkun nettoarvo on (90d).

Jos haluat salkkujesi arvon pysyvän samana riippumatta siitä, mihin taustalla oleva osakekurssi menee, salkun arvon pitäisi pysyä samana kummassakin tapauksessa:

$\begin{matrix} h. (d.) - m. = l. (d.) \\ missä: \\ h. = Korkein mahdollinen taustalla oleva hinta. \\ d. = Osakkeiden lukumäärä. \\ m. = Rahat menetettiin lyhyen puhelun takaisinmaksun yhteydessä. \\ l. = Alin mahdollinen taustalla oleva hinta. \end{matrix}$ h(d)−m=l(d)missä:h=Korkein mahdollinen taustalla oleva hintad=Osakkeiden lukumääräm=Rahat menetettiin lyhyen puhelun takaisinmaksun yhteydessäl=Alin mahdollinen taustalla oleva hinta

Joten jos ostat puolet osakkeesta, olettaen, että osittaiset ostot ovat mahdollisia, onnistut luomaan niin, että sen arvo pysyy samana molemmissa mahdollisissa tiloissa tietyn ajan kuluessa vuosi.

$\begin{matrix} 1. 1. 0. d. - 1. 0. = 9. 0. d. \\ d. = \frac{1.}{2.} \end{matrix}$ 110d−10=90dd=21

Tämä salkun arvo, joka on merkitty (90d) tai (110d - 10) = 45, on vuotta alempana. Sen laskemiseksi nykyarvo, sen voi alentaa riskitön korko tuottoa (olettaen 5%).

$\begin{matrix} Nykyarvo. & = 9. 0. d. \times {e.}^{(- 5. % \times 1. Vuosi.)} \\ = 4. 5. \times 0. . 9. 5. 2. 3. \\ = 4. 2. . 8. 5. \end{matrix}$ Nykyarvo=90d×e(−5%×1 Vuosi)=45×0.9523=42.85

Koska tällä hetkellä salkku koostuu ½ osasta kohde -etuutena olevia osakkeita (markkinahinta 100 dollaria) ja yhdestä lyhyestä puhelusta, sen pitäisi olla yhtä suuri kuin nykyarvo.

$\begin{matrix} \frac{1.}{2.} \times 1. 0. 0. - 1. \times Soita Hinta. = $ 4. 2. . 8. 5. \\ Soita Hinta. = $ 7. . 1. 4. eli tämän päivän puheluhinta. \end{matrix}$ 21×100−1×Soita Hinta=$42.85Soita Hinta=$7.14eli tämän päivän puheluhinta

Koska tämä perustuu olettamukseen, että salkun arvo pysyy samana riippumatta siitä, mihin kohde -etuus kulkee, ylös- tai alas -liikkeen todennäköisyydellä ei ole mitään merkitystä. Salkku pysyy riskittömänä taustalla olevista hintamuutoksista riippumatta.

Molemmissa tapauksissa (oletetaan nousevan ylöspäin 110 dollariin ja alaspäin 90 dollariin) portfoliosi on neutraali riskille ja ansaitsee riskittömän tuottoaste.

Näin ollen molemmat kauppiaat, Peter ja Paula, olisivat valmiita maksamaan saman 7,14 dollaria tästä ostovaihtoehdosta, vaikka heidän käsityksensä ylöspäin suuntautuvien muutosten todennäköisyydestä ovat erilaiset (60% ja 40%). Niiden yksilöllisillä todennäköisyyksillä ei ole merkitystä optioiden arvioinnissa.

Olettaen sen sijaan, että yksittäisillä todennäköisyyksillä on merkitystä, arbitraasimahdollisuudet ovat saattaneet ilmaantua. Todellisessa maailmassa tällaisia arbitraasimahdollisuuksia on pienillä hintaeroilla ja ne katoavat Lyhytaikainen.

Mutta missä on kaikkien näiden laskelmien kiihkeä volatiliteetti, tärkeä ja arkaluonteinen tekijä, joka vaikuttaa optioiden hinnoitteluun?

The volatiliteetti sisältyy jo ongelman määritelmän luonteeseen. Jos oletetaan kaksi (ja vain kaksi - tästä syystä nimi "binomi") hintatasoa (110 dollaria ja 90 dollaria), volatiliteetti on implisiittinen tässä oletuksessa ja sisältyy automaattisesti (10% kumpaankin suuntaan tässä esimerkissä).

Musta-Scholes

Mutta onko tämä lähestymistapa oikea ja johdonmukainen yleisesti käytetyn Black-Scholes-hinnoittelun kanssa? Vaihtoehdot -laskimen tulokset (OIC: n hyväksi) vastaavat tarkasti laskettua arvoa:

Valitettavasti todellinen maailma ei ole niin yksinkertainen kuin ”vain kaksi valtiota”. Varasto voi nousta useille hintatasoille ennen sen päättymistä.

Onko mahdollista sisällyttää kaikki nämä useat tasot binomiseen hinnoittelumalliin, joka on rajoitettu vain kahteen tasoon? Kyllä, se on hyvin mahdollista, mutta sen ymmärtäminen vaatii yksinkertaista matematiikkaa.

Yksinkertainen matematiikka

Yleistää tämän ongelman ja ratkaisun:

"X" on osakkeen nykyinen markkinahinta ja "X*u" ja "X*d" ovat tulevia hintoja ylös- ja alaspäin suuntautuvista muutoksista "t" vuotta myöhemmin. Kerroin "u" on suurempi kuin yksi, koska se osoittaa ylöspäin suuntautuvan liikkeen ja "d" on nollan ja yhden välissä. Yllä olevassa esimerkissä u = 1,1 ja d = 0,9.

Osto -optioiden voitot ovat "P_ylös"ja" P._dn"ylös ja alas liikkuu voimassaolon päättymishetkellä.

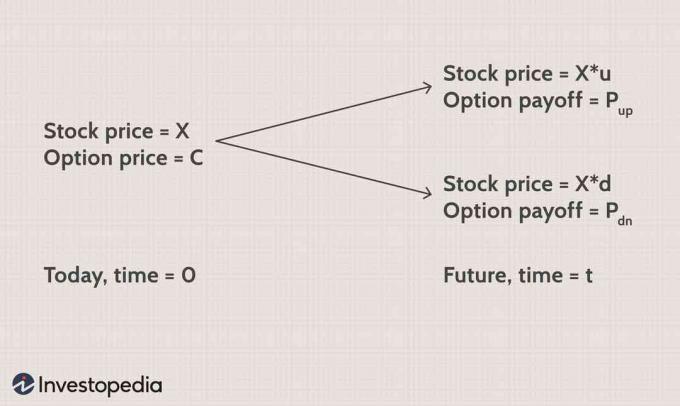
Jos rakennat salkun tänään ostettuja "s" -osakkeita ja lyhyen yhden optio -oikeuden, niin "t" -ajan jälkeen:

$\begin{matrix} VUM. = s. \times X. \times u. - {P.}_{ylös.} \\ missä: \\ VUM. = Salkun arvo nousun yhteydessä. \end{matrix}$ VUM=s×X×u−Pylösmissä:VUM=Salkun arvo nousun yhteydessä

$\begin{matrix} VDM. = s. \times X. \times d. - {P.}_{alas.} \\ missä: \\ VDM. = Salkun arvo alaspäin suuntautuvan liikkeen tapauksessa. \end{matrix}$ VDM=s×X×d−Palasmissä:VDM=Salkun arvo alaspäin suuntautuvan liikkeen tapauksessa

Samanlainen arviointi kummassakin hinnamuutoksen tapauksessa:

$s. \times X. \times u. - {P.}_{ylös.} = s. \times X. \times d. - {P.}_{alas.}$ s×X×u−Pylös=s×X×d−Palas

$\begin{matrix} s. & = \frac{{P.}_{ylös.} - {P.}_{alas.}}{X. \times (u. - d.)} \\ = Ostettavien osakkeiden lukumäärä. \\ riskitön portfolio. \end{matrix}$ s=X×(u−d)Pylös−Palas=Ostettavien osakkeiden lukumäärä=riskitön portfolio

Salkun tuleva arvo "t" vuosien lopussa on:

$\begin{matrix} Ylösliikkeen tapauksessa. & = s. \times X. \times u. - {P.}_{ylös.} \\ = \frac{{P.}_{ylös.} - {P.}_{alas.}}{u. - d.} \times u. - {P.}_{ylös.} \end{matrix}$ Ylösliikkeen tapauksessa=s×X×u−Pylös=u−dPylös−Palas×u−Pylös

$\begin{matrix} Alaspäin siirron tapauksessa. & = s. \times X. \times d. - {P.}_{alas.} \\ = \frac{{P.}_{ylös.} - {P.}_{alas.}}{u. - d.} \times d. - {P.}_{alas.} \end{matrix}$ Alaspäin siirron tapauksessa=s×X×d−Palas=u−dPylös−Palas×d−Palas

Tämän päivän arvo saadaan diskonttaamalla se riskittömään tuottoon:

$\begin{matrix} PV. = e. (- r. t.) \times [\frac{{P.}_{ylös.} - {P.}_{alas.}}{u. - d.} \times u. - {P.}_{ylös.}] \\ missä: \\ PV. = Tämän päivän arvo. \\ r. = Palautusaste. \\ t. = Aika, vuosina. \end{matrix}$ PV=e(−rt)×[u−dPylös−Palas×u−Pylös]missä:PV=Tämän päivän arvor=Palautusastet=Aika, vuosina

Tämän pitäisi vastata "s" -osakkeiden salkunomistusta X -hinnalla ja lyhyen puhelun arvo "c" (nykyinen omistusosuus (s* X - c) vastaa tätä laskentaa.) "C" -ratkaisun antaminen antaa sen lopulta kuten:

Huomautus: Jos puhelupalkkio on oikosulussa, sen on oltava lisäys salkkuun, ei vähennys.

$c. = \frac{e. (- r. t.)}{u. - d.} \times [(e. (- r. t.) - d.) \times {P.}_{ylös.} + (u. - e. (- r. t.)) \times {P.}_{alas.}]$ c=u−de(−rt)×[(e(−rt)−d)×Pylös+(u−e(−rt))×Palas]

Toinen tapa kirjoittaa yhtälö on järjestää se uudelleen:

Käyttämällä "q":

$q. = \frac{e. (- r. t.) - d.}{u. - d.}$ q=u−de(−rt)−d

Sitten yhtälö tulee:

$c. = e. (- r. t.) \times (q. \times {P.}_{ylös.} + (1. - q.) \times {P.}_{alas.})$ c=e(−rt)×(q×Pylös+(1−q)×Palas)

Yhtälön järjestäminen uudelleen q: n suhteen on tarjonnut uuden näkökulman.

Nyt voit tulkita ”q” todennäköisyytenä kohde -etuuden nousulle (koska ”q” liittyy P: hen_ylös ja "1-q" liittyy P: hen_dn). Kaiken kaikkiaan yhtälö edustaa nykypäivää option hinta, sen voiton diskontattu arvo päättyessä.

Tämä "Q" on erilainen

Miten tämä todennäköisyys "q" eroaa taustalla olevan ylös- tai alaspäin suuntautuvan liikkeen todennäköisyydestä?

$\begin{matrix} VSP. = q. \times X. \times u. + (1. - q.) \times X. \times d. \\ missä: \\ VSP. = Osakekurssin arvo ajankohtana. t. \end{matrix}$ VSP=q×X×u+(1−q)×X×dmissä:VSP=Osakekurssin arvo ajankohtana t

Korvaamalla arvon "q" ja järjestämällä sen uudelleen, osakekurssi ajankohtana "t" tulee:

$\begin{matrix} Osakekurssi. = e. (r. t.) \times X. \end{matrix}$ Osakekurssi=e(rt)×X

Tässä oletetussa kahden valtion maailmassa osakekurssi yksinkertaisesti nousee riskittömän tuoton verran, aivan kuten riskitön omaisuus, ja siksi se pysyy riippumattomana kaikista riskeistä. Sijoittajat ovat välinpitämättömiä tämän mallin riskeille, joten tämä on riskineutraali malli.

Todennäköisyys "q" ja "(1-q)" tunnetaan riskineutraaleina todennäköisyyksinä ja arvostusmenetelmä tunnetaan riskineutraalina arvostusmallina.

Esimerkkiskenaariossa on yksi tärkeä vaatimus - tulevaa voittorakennetta vaaditaan tarkasti (tasot 110 ja 90 dollaria). Tosielämässä tällainen selkeys askelpoisista hintatasoista ei ole mahdollista; pikemminkin hinta liikkuu satunnaisesti ja voi asettua useille tasoille.

Laajenna esimerkkiä edelleen olettaen, että kaksivaiheiset hintatasot ovat mahdollisia. Tiedämme toisen vaiheen lopulliset voitot ja meidän on arvostettava vaihtoehto tänään (ensimmäisessä vaiheessa):

Taaksepäin toimiessa ensimmäisen vaiheen väliarviointi (t = 1) voidaan tehdä käyttämällä lopullisia voittoja vaiheessa 2 (t = 2), sitten käyttämällä näitä laskettuja ensimmäisen vaiheen arvostuksia (t = 1), nykyinen arvostus (t = 0) voidaan saavuttaa näillä laskelmia.

Optioiden hinnoittelun saamiseksi toisella sijalla käytetään voittoja neljällä ja viidellä. Kolmannen hinnan saamiseksi käytetään voittoja viidellä ja kuudella. Lopuksi laskettuja voittoja kahdessa ja kolmessa käytetään hinnoittelussa ykkösenä.

Huomaa, että tässä esimerkissä oletetaan sama tekijä ylös- (ja alas) -liikkeille molemmissa vaiheissa - u ja d on yhdistetty.

Toimiva esimerkki

Oletetaan, että a myyntioptio Lakkohinta 110 dollaria on tällä hetkellä kaupankäynnin kohteena 100 dollaria ja vanhenee vuoden kuluttua. Vuotuinen riskitön korko on 5%. Hintojen odotetaan nousevan 20% ja laskevan 15% kuuden kuukauden välein.

Tässä u = 1,2 ja d = 0,85, x = 100, t = 0,5.

käyttämällä yllä olevaa johdettua kaavaa.

$q. = \frac{e. (- r. t.) - d.}{u. - d.}$ q=u−de(−rt)−d

saamme q = 0,35802832.

myyntioption arvo kohdassa 2,

$\begin{matrix} {s.}_{2.} = e. (- r. t.) \times (s. \times {P.}_{ylös ylös.} + (1. - q.) {P.}_{päivitys}) \\ missä: \\ s. = Myyntivaihtoehdon hinta. \end{matrix}$ s2=e(−rt)×(s×Pylös ylös+(1−q)Ppäivitys)missä:s=Myyntivaihtoehdon hinta

Osoitteessa P._{ylös ylös} ehto, taustalla on = 100*1,2*1,2 = 144 dollaria, joka johtaa P: hen_{ylös ylös}= nolla.

Osoitteessa P._päivitys ehto, taustalla on = 100*1,2*0,85 = 102 dollaria, joka johtaa P: hen_päivitys= $8.

Osoitteessa P._dndn ehto, taustalla on = 100*0,85*0,85 = 72,25 dollaria, joka johtaa P: hen_dndn= $37.75.

s₂ = 0.975309912*(0.35802832*0+(1-0.35802832)*8) = 5.008970741.

Samoin s₃ = 0.975309912*(0.35802832*8+(1-0.35802832)*37.75) = 26.42958924.

${s.}_{1.} = e. (- r. t.) \times (q. \times {s.}_{2.} + (1. - q.) {s.}_{3.})$ s1=e(−rt)×(q×s2+(1−q)s3)

Ja siksi myyntioption arvo, s₁ = 0.975309912*(0.35802832*5.008970741+(1-0.35802832)* 26.42958924) = $18.29.

Samoin binomimallien avulla voit katkaista koko vaihtoehdon keston useiden vaiheiden ja tasojen tarkentamiseksi. Tietokoneohjelmien tai laskentataulukoiden avulla voit siirtyä taaksepäin askel kerrallaan saadaksesi halutun vaihtoehdon nykyarvon.

Toinen esimerkki

Oletetaan eurooppalaistyyppinen myyntioptio, jonka voimassaolo päättyy yhdeksän kuukautta, merkintähinta 12 dollaria ja nykyinen taustalla oleva hinta 10 dollaria. Oletetaan 5%: n riskitön korko kaikille kausille. Oletetaan, että kolmen kuukauden välein taustalla oleva hinta voi liikkua 20% ylös tai alas, jolloin saadaan u = 1,2, d = 0,8, t = 0,25 ja kolmivaiheinen binomipuu.

Punainen osoittaa taustalla olevia hintoja ja sininen osoittaa myyntioptioiden voittoa.

Riskineutraali todennäköisyys "q" on 0,531446.

Käyttämällä yllä olevaa arvoa "q" ja voittoarvoja t = yhdeksän kuukautta, vastaavat arvot t = kuusi kuukautta lasketaan seuraavasti:

Lisäksi käyttämällä näitä laskettuja arvoja t = 6, arvot t = 3 ja sitten t = 0 ovat:

Tämä antaa myyntioption nykypäivän arvon 2,18 dollariksi, joka on melko lähellä sitä, mitä Black-Scholes-mallia käyttäen laskettaessa (2,30 dollaria).

Bottom Line

Vaikka tietokoneohjelmien käyttö voi tehdä nämä intensiiviset laskelmat helpoksi, tulevien hintojen ennustaminen on edelleen binomimallien merkittävä rajoitus vaihtoehtojen hinnoittelulle. Mitä lyhyemmät aikavälit ovat, sitä vaikeampaa on ennustaa voitot kunkin jakson lopussa korkealla tarkkuudella.

Joustavuus sisällyttää eri aikoina odotetut muutokset on kuitenkin plus, mikä tekee siitä sopivan hinnoitteluun Amerikkalaisia vaihtoehtoja, mukaan lukien varhaisen käytön arvioinnit.

Binomimallilla lasketut arvot vastaavat tarkasti muiden yleisesti käytettyjen arvoja malleja, kuten Black-Scholes, mikä osoittaa binomimallien käyttökelpoisuuden ja tarkkuuden hinnoittelu. Binomihinnoittelumallit voidaan kehittää elinkeinonharjoittajan mieltymysten mukaan ja ne voivat toimia vaihtoehtona Black-Scholesille.