Compreendendo o modelo de precificação de opção binomial

Determinando os preços das ações

Chegar a um acordo sobre preços precisos para qualquer ativo negociável é um desafio - é por isso que os preços das ações mudam constantemente. Na realidade, as empresas dificilmente mudam seus avaliações no dia-a-dia, mas os preços e avaliações de suas ações mudam quase a cada segundo. Esta dificuldade em chegar a um consenso sobre o preço correto para qualquer ativo negociável leva a arbitragem oportunidades.

Mas muitos investimentos bem-sucedidos se resumem a uma simples questão de avaliação atual - o que é o certo preço atual hoje para uma recompensa futura esperada?

Principais vantagens

O modelo de precificação de opção binomial avalia as opções usando uma abordagem iterativa, utilizando vários períodos para avaliar as opções americanas.
Com o modelo, há dois resultados possíveis com cada iteração - um movimento para cima ou para baixo que segue uma árvore binomial.
O modelo é intuitivo e é usado com mais frequência na prática do que o conhecido modelo Black-Scholes.

instagram viewer

Avaliação de opções binomiais

Em um mercado competitivo, para evitar oportunidades de arbitragem, ativos com estruturas de payoff idênticas devem ter o mesmo preço. Avaliação de opções tem sido uma tarefa desafiadora e variações de preços levam a oportunidades de arbitragem. Black-Scholes continua a ser um dos modelos mais populares usados para precificação opções mas tem limitações.

O preço de opção binomial modelo é outro método popular usado para opções de preços.

Exemplos

Suponha que haja um opção de chamada em um determinado estoque com uma corrente preço de mercado de $ 100. O no dinheiro (ATM) opção tem um preço de exercício de $ 100 com prazo de validade de um ano. Existem dois corretores, Peter e Paula, que concordam que o preço das ações subirá para US $ 110 ou cairá para US $ 90 em um ano.

Eles concordam sobre os níveis de preços esperados em um determinado período de um ano, mas discordam sobre a probabilidade de um movimento para cima ou para baixo. Peter acredita que a probabilidade de o preço da ação subir para US $ 110 é de 60%, enquanto Paula acredita que é de 40%.

Com base nisso, quem estaria disposto a pagar mais preço pela opção de compra? Possivelmente Peter, pois ele espera uma alta probabilidade de movimento para cima.

Cálculos de opções binomiais

Os dois ativos, dos quais a avaliação depende, são a opção de compra e o estoque subjacente. Há um acordo entre os participantes de que o preço da ação subjacente pode passar dos atuais $ 100 para $ 110 ou $ 90 em um ano e não há outros movimentos de preço possíveis.

Em um mundo livre de arbitragem, se você tiver que criar uma carteira composta por esses dois ativos, opção de compra e ações subjacentes, de modo que, independentemente de para onde vá o preço subjacente - $ 110 ou $ 90 - o retorno líquido da carteira sempre permanece o mesmo. Suponha que você compre ações "d" de opções de compra subjacentes e vendidas em uma única opção para criar esse portfólio.

Se o preço chegar a $ 110, suas ações valerão $ 110 * d, e você perderá $ 10 no chamada curta Pague. O valor líquido do seu portfólio será (110d - 10).

Se o preço cair para $ 90, suas ações valerão $ 90 * d, e a opção expirará sem valor. O valor líquido do seu portfólio será (90d).

Se você deseja que o valor do seu portfólio permaneça o mesmo, independentemente de para onde vai o preço das ações subjacentes, então o valor do seu portfólio deve permanecer o mesmo em ambos os casos:

$\begin{matrix} h. (d.) - m. = eu. (d.) \\ Onde: \\ h. = Preço subjacente potencial mais alto. \\ d. = Número de ações subjacentes. \\ m. = Dinheiro perdido no pagamento de chamadas curtas. \\ eu. = Menor preço subjacente potencial. \end{matrix}$ h(d)−m=eu(d)Onde:h=Preço subjacente potencial mais altod=Número de ações subjacentesm=Dinheiro perdido no pagamento de chamadaseu=Menor preço subjacente potencial

Portanto, se você comprar meia ação, assumindo que as compras fracionárias são possíveis, você conseguirá criar um carteira de modo que seu valor permaneça o mesmo em ambos os estados possíveis dentro do prazo determinado de um ano.

$\begin{matrix} 1. 1. 0. d. - 1. 0. = 9. 0. d. \\ d. = \frac{1.}{2.} \end{matrix}$ 110d−10=90dd=21

Este valor de portfólio, indicado por (90d) ou (110d - 10) = 45, está um ano depois da linha. Para calcular o seu valor presente, pode ser descontado pelo taxa livre de risco de retorno (assumindo 5%).

$\begin{matrix} Valor presente. & = 9. 0. d. \times {e.}^{(- 5. % \times 1. Ano.)} \\ = 4. 5. \times 0. . 9. 5. 2. 3. \\ = 4. 2. . 8. 5. \end{matrix}$ Valor presente=90d×e(−5%×1 Ano)=45×0.9523=42.85

Uma vez que, atualmente, a carteira é composta por ½ ação do estoque subjacente (com um preço de mercado de $ 100) e uma opção de compra, deve ser igual ao valor presente.

$\begin{matrix} \frac{1.}{2.} \times 1. 0. 0. - 1. \times Preço da chamada. = $ 4. 2. . 8. 5. \\ Preço da chamada. = $ 7. . 1. 4., ou seja, o preço da chamada de hoje. \end{matrix}$ 21×100−1×Preço de Chamada=$42.85Preço de Chamada=$7.14, ou seja, o preço da chamada de hoje

Uma vez que isso se baseia na suposição de que o valor da carteira permanece o mesmo, independentemente da direção do preço subjacente, a probabilidade de um movimento para cima ou para baixo não desempenha nenhum papel. A carteira permanece livre de risco, independentemente dos movimentos de preço subjacentes.

Em ambos os casos (assumido para mover para cima para $ 110 e para baixo para mover para $ 90), sua carteira é neutra ao risco e ganha o livre de risco taxa de retorno.

Portanto, ambos os negociantes, Peter e Paula, estariam dispostos a pagar os mesmos $ 7,14 por esta opção de compra, apesar de suas diferentes percepções das probabilidades de movimentos de alta (60% e 40%). Suas probabilidades percebidas individualmente não importam na avaliação de opções.

Supondo, em vez disso, que as probabilidades individuais importam, as oportunidades de arbitragem podem ter se apresentado. No mundo real, essas oportunidades de arbitragem existem com pequenos diferenciais de preço e desaparecem no curto prazo.

Mas onde está a tão alardeada volatilidade em todos esses cálculos, um fator importante e sensível que afeta o preço das opções?

O volatilidade já está incluído pela natureza da definição do problema. Supondo dois (e apenas dois - daí o nome “binomial”) estados de níveis de preços ($ 110 e $ 90), a volatilidade está implícita nesta suposição e incluída automaticamente (10% de qualquer forma neste exemplo).

Black-Scholes

Mas essa abordagem é correta e coerente com os preços comumente usados de Black-Scholes? Os resultados da calculadora de opções (cortesia da OIC) correspondem de perto ao valor calculado:

Infelizmente, o mundo real não é tão simples quanto “apenas dois estados”. O estoque pode atingir vários níveis de preço antes de expirar.

É possível incluir todos esses níveis múltiplos em um modelo de precificação binomial restrito a apenas dois níveis? Sim, é muito possível, mas para entendê-lo é preciso um pouco de matemática simples.

Matemática simples

Para generalizar este problema e solução:

"X" é o preço de mercado atual de uma ação e "X * u" e "X * d" são os preços futuros para movimentos de alta e baixa "t" anos depois. O fator "u" será maior do que um, pois indica um movimento para cima e "d" ficará entre zero e um. Para o exemplo acima, u = 1,1 ed = 0,9.

Os pagamentos das opções de compra são "P_{pra cima}" e P_dn"para movimentos para cima e para baixo no momento da expiração.

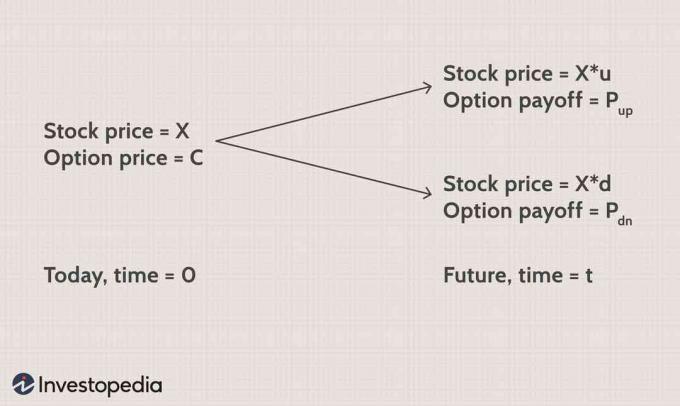
Imagem de Sabrina Jiang © Investopedia 2020

Se você construir uma carteira de ações "s" adquiridas hoje e vender uma opção de compra, depois do tempo "t":

$\begin{matrix} VUM. = s. \times X. \times você. - {P.}_{pra cima.} \\ Onde: \\ VUM. = Valor da carteira em caso de aumento. \end{matrix}$ VUM=s×X×você−Ppra cimaOnde:VUM=Valor do portfólio em caso de movimento ascendente

$\begin{matrix} VDM. = s. \times X. \times d. - {P.}_{baixa.} \\ Onde: \\ VDM. = Valor da carteira em caso de queda. \end{matrix}$ VDM=s×X×d−PbaixaOnde:VDM=Valor da carteira em caso de queda

Para avaliação semelhante em qualquer caso de movimento de preço:

$s. \times X. \times você. - {P.}_{pra cima.} = s. \times X. \times d. - {P.}_{baixa.}$ s×X×você−Ppra cima=s×X×d−Pbaixa

$\begin{matrix} s. & = \frac{{P.}_{pra cima.} - {P.}_{baixa.}}{X. \times (você. - d.)} \\ = O número de ações a serem compradas. \\ uma carteira livre de risco. \end{matrix}$ s=X×(você−d)Ppra cima−Pbaixa=O número de ações a serem compradas=um portfólio livre de risco

O valor futuro da carteira ao final de "t" anos será:

$\begin{matrix} Em caso de movimento para cima. & = s. \times X. \times você. - {P.}_{pra cima.} \\ = \frac{{P.}_{pra cima.} - {P.}_{baixa.}}{você. - d.} \times você. - {P.}_{pra cima.} \end{matrix}$ Em caso de movimento para cima=s×X×você−Ppra cima=você−dPpra cima−Pbaixa×você−Ppra cima

$\begin{matrix} Em caso de movimento para baixo. & = s. \times X. \times d. - {P.}_{baixa.} \\ = \frac{{P.}_{pra cima.} - {P.}_{baixa.}}{você. - d.} \times d. - {P.}_{baixa.} \end{matrix}$ Em caso de movimento para baixo=s×X×d−Pbaixa=você−dPpra cima−Pbaixa×d−Pbaixa

O valor atual pode ser obtido descontando-o com a taxa de retorno livre de risco:

$\begin{matrix} PV. = e. (- r. t.) \times [\frac{{P.}_{pra cima.} - {P.}_{baixa.}}{você. - d.} \times você. - {P.}_{pra cima.}] \\ Onde: \\ PV. = Valor atual. \\ r. = Taxa de retorno. \\ t. = Tempo, em anos. \end{matrix}$ PV=e(−rt)×[você−dPpra cima−Pbaixa×você−Ppra cima]Onde:PV=Valor Atualr=Taxa de retornot=Tempo, em anos

Isso deve coincidir com a carteira de ações "s" ao preço X, e o valor de compra "c" (a participação atual de (s * X - c) deve ser igual a este cálculo.) Resolvendo para "c" finalmente resulta Como:

Nota: Se o prêmio da chamada for vendido, deve ser um acréscimo ao portfólio, não uma subtração.

$c. = \frac{e. (- r. t.)}{você. - d.} \times [(e. (- r. t.) - d.) \times {P.}_{pra cima.} + (você. - e. (- r. t.)) \times {P.}_{baixa.}]$ c=você−de(−rt)×[(e(−rt)−d)×Ppra cima+(você−e(−rt))×Pbaixa]

Outra maneira de escrever a equação é reorganizá-la:

Tomando "q" como:

$q. = \frac{e. (- r. t.) - d.}{você. - d.}$ q=você−de(−rt)−d

Então a equação se torna:

$c. = e. (- r. t.) \times (q. \times {P.}_{pra cima.} + (1. - q.) \times {P.}_{baixa.})$ c=e(−rt)×(q×Ppra cima+(1−q)×Pbaixa)

Reorganizar a equação em termos de “q” ofereceu uma nova perspectiva.

Agora você pode interpretar “q” como a probabilidade do movimento para cima do subjacente (como “q” está associado a P_{pra cima} e “1-q” está associado a P_dn). No geral, a equação representa a atual preço da opção, o valor descontado de seu pagamento no vencimento.

Este "Q" é diferente

Como essa probabilidade “q” difere da probabilidade de um movimento para cima ou para baixo do subjacente?

$\begin{matrix} VSP. = q. \times X. \times você. + (1. - q.) \times X. \times d. \\ Onde: \\ VSP. = Valor do preço das ações no momento. t. \end{matrix}$ VSP=q×X×você+(1−q)×X×dOnde:VSP=Valor do preço das ações no momento t

Substituindo o valor de "q" e reorganizando, o preço da ação no momento "t" chega a:

$\begin{matrix} Preço das ações. = e. (r. t.) \times X. \end{matrix}$ Preço da ação=e(rt)×X

Nesse mundo presumido de dois estados, o preço das ações simplesmente aumenta pela taxa de retorno sem risco, exatamente como um ativo sem risco e, portanto, permanece independente de qualquer risco. Os investidores são indiferentes ao risco sob este modelo, portanto, este constitui o modelo neutro ao risco.

Probabilidades “q” e “(1-q)” são conhecidas como probabilidades neutras ao risco e o método de avaliação é conhecido como modelo de avaliação neutro ao risco.

O cenário de exemplo tem um requisito importante - a estrutura de recompensa futura é exigida com precisão (nível $ 110 e $ 90). Na vida real, essa clareza sobre os níveis de preços baseados em etapas não é possível; em vez disso, o preço se move aleatoriamente e pode ser liquidado em vários níveis.

Para expandir ainda mais o exemplo, suponha que os níveis de preços em duas etapas sejam possíveis. Conhecemos os resultados finais da segunda etapa e precisamos avaliar a opção hoje (na etapa inicial):

Trabalhando para trás, a avaliação da primeira etapa intermediária (em t = 1) pode ser feita usando os payoffs finais na etapa dois (t = 2), então usando esta avaliação calculada da primeira etapa (t = 1), a avaliação atual (t = 0) pode ser alcançada com estes cálculos.

Para obter o preço das opções no número dois, são usados os payoffs em quatro e cinco. Para obter o preço do número três, são usados os pagamentos de cinco e seis. Finalmente, os payoffs calculados em dois e três são usados para obter preços no número um.

Observe que este exemplo assume o mesmo fator para movimentos para cima (e para baixo) em ambas as etapas - ued são aplicados de forma composta.

Um exemplo prático

Suponha que um opção de colocar com um preço de exercício de $ 110, está sendo negociado atualmente a $ 100 e expira em um ano. A taxa anual livre de risco é de 5%. O preço deve aumentar 20% e diminuir 15% a cada seis meses.

Aqui, u = 1,2 ed = 0,85, x = 100, t = 0,5.

usando a fórmula derivada acima de.

$q. = \frac{e. (- r. t.) - d.}{você. - d.}$ q=você−de(−rt)−d

obtemos q = 0,35802832.

valor da opção de venda no ponto 2,

$\begin{matrix} {p.}_{2.} = e. (- r. t.) \times (p. \times {P.}_{acima, acima.} + (1. - q.) {P.}_{Updn.}) \\ Onde: \\ p. = Preço da opção de venda. \end{matrix}$ p2=e(−rt)×(p×Pacima, acima+(1−q)Patualização)Onde:p=Preço da opção de venda

Em P_{acima, acima} condição, subjacente será = 100 * 1,2 * 1,2 = $ 144 levando a P_{acima, acima}= zero.

Em P_{atualização} condição, subjacente será = 100 * 1,2 * 0,85 = $ 102 levando a P_{atualização}= $8.

Em P_dndn condição, subjacente será = 100 * 0,85 * 0,85 = $ 72,25 levando a P_dndn= $37.75.

p₂ = 0.975309912*(0.35802832*0+(1-0.35802832)*8) = 5.008970741.

Da mesma forma, p₃ = 0.975309912*(0.35802832*8+(1-0.35802832)*37.75) = 26.42958924.

${p.}_{1.} = e. (- r. t.) \times (q. \times {p.}_{2.} + (1. - q.) {p.}_{3.})$ p1=e(−rt)×(q×p2+(1−q)p3)

E, portanto, o valor da opção de venda, p₁ = 0.975309912*(0.35802832*5.008970741+(1-0.35802832)* 26.42958924) = $18.29.

Da mesma forma, os modelos binomiais permitem quebrar toda a duração da opção para várias etapas e níveis refinados. Usando programas de computador ou planilhas, você pode retroceder um passo de cada vez para obter o valor presente da opção desejada.

Outro exemplo

Suponha uma opção de venda do tipo europeu com nove meses até o vencimento, um preço de exercício de $ 12 e um preço subjacente atual de $ 10. Suponha uma taxa livre de risco de 5% para todos os períodos. Suponha que a cada três meses, o preço subjacente pode mover-se 20% para cima ou para baixo, dando-nos u = 1,2, d = 0,8, t = 0,25 e três etapas árvore binomial.

O vermelho indica os preços subjacentes, enquanto o azul indica o retorno das opções de venda.

A probabilidade neutra ao risco "q" é calculada em 0,531446.

Usando o valor de "q" acima e os valores de payoff em t = nove meses, os valores correspondentes em t = seis meses são calculados como:

Além disso, usando esses valores calculados em t = 6, os valores em t = 3, em seguida, em t = 0 são:

Isso dá o valor atual de uma opção de venda como $ 2,18, muito próximo do que você encontraria fazendo os cálculos usando o modelo de Black-Scholes ($ 2,30).

The Bottom Line

Embora o uso de programas de computador possa facilitar esses cálculos intensivos, a previsão de preços futuros continua sendo uma das principais limitações dos modelos binomiais de precificação de opções. Quanto mais precisos os intervalos de tempo, mais difícil será prever os ganhos no final de cada período com precisão de alto nível.

No entanto, a flexibilidade para incorporar as mudanças esperadas em diferentes períodos é um diferencial, o que o torna adequado para precificação Opções americanas, incluindo avaliações de exercício antecipado.

Os valores calculados usando o modelo binomial correspondem de perto aos calculados a partir de outros comumente usados modelos como Black-Scholes, que indica a utilidade e precisão dos modelos binomiais para opção preços. Os modelos de precificação binomial podem ser desenvolvidos de acordo com as preferências do trader e podem funcionar como uma alternativa ao Black-Scholes.