Pariați mai inteligent cu simularea Monte Carlo
În finanțe, există o cantitate echitabilă de incertitudine și risc implicate în estimarea valoarea viitoare de cifre sau sume datorate varietății largi de rezultate potențiale. Simulare Monte Carlo (MCS) este o tehnică care ajută la reducerea incertitudinii implicate în estimarea rezultatelor viitoare. MCS poate fi aplicat modelelor complexe, neliniare sau utilizat pentru a evalua acuratețea și performanța altor modele. Poate fi, de asemenea, implementat în managementul riscurilor, gestionarea portofoliului, stabilirea prețurilor instrumentelor derivate, planificarea strategică, planificarea proiectelor, modelarea costurilor și alte domenii.
Definiția MCS
MCS este o tehnică care convertește incertitudinile în variabilele de intrare ale unui model în distribuții de probabilitate. Prin combinarea distribuțiilor și selectarea aleatorie a valorilor din acestea, recalculează modelul simulat de multe ori și scoate la iveală probabilitatea ieșirii.
Caracteristici de bază
- MCS permite utilizarea mai multor intrări în același timp pentru a crea distribuția de probabilitate a uneia sau mai multor ieșiri.
- Diferite tipuri de distribuții de probabilitate pot fi atribuite intrărilor modelului. Când distribuția este necunoscută, ar putea fi aleasă cea care reprezintă cea mai bună potrivire.
- Utilizarea numerelor aleatorii caracterizează MCS ca fiind stochastic metodă. Numerele aleatorii trebuie să fie independente; Nu corelație ar trebui să existe între ei.
- MCS generează ieșirea ca un interval în loc de o valoare fixă și arată cât de probabil este ca valoarea ieșirii să apară în interval.
Unele distribuții de probabilități utilizate frecvent în MCS
Distribuție normală / gaussiană: Distribuție continuă aplicată în situații în care media și deviație standard sunt date și media reprezintă cea mai probabilă valoare a variabilei. Este simetric în jurul valorii medii și nu este delimitat.
Distribuție cognitivă: Distribuție continuă specificată prin deviație medie și standard. Acest lucru este adecvat pentru o variabilă de la zero la infinit, cu pozitiv asimetrie și cu un logaritm natural distribuit în mod normal.
Distribuție triunghiulară: Distribuție continuă cu valori minime și maxime fixe. Este delimitat de valorile minime și maxime și poate fi fie simetrică (cea mai probabilă valoare = medie = mediană), fie asimetrică.
Distributie uniforma: Distribuție continuă delimitată de valorile minime și maxime cunoscute. Spre deosebire de distribuția triunghiulară, probabilitatea apariției valorilor între minim și maxim este aceeași.
Distribuție exponențială: Distribuție continuă utilizată pentru a ilustra timpul dintre aparițiile independente, cu condiția să se cunoască rata aparițiilor.
Matematica din spatele MCS
Luați în considerare faptul că avem o funcție cu valoare reală g (X) cu funcția de frecvență de probabilitate P (x) (dacă X este discretă), sau funcția de densitate de probabilitate f (x) (dacă X este continuu). Apoi putem defini valoarea așteptată a lui g (X) în termeni discreți și, respectiv, continuați:
E(g(X))=−∞∑+∞g(X)P(X), Unde P(X)>0 și−∞∑+∞P(X)=1E(g(X))=∫−∞+∞g(X)f(X)dX, Unde f(X)>0 și ∫−∞+∞f(X)dX=1Apoi, faceți n desene aleatorii ale X(X1,…,Xn), numitprobe sau simulări, calculați g(X1),…,g(Xn)și găsiți media g(X) din eșantion:
gnμ(X)=n1eu=1∑ng(Xeu), care reprezintă finalul simulatvaloarea E(g(X)).Prin urmare gnμ(X)=n1eu=1∑ng(X) va fi Monte Carloestimator al E(g(X)).La fel de n→∞,gnμ(X)→E(g(X)),astfel putem acumcalculați dispersia în jurul valorii medii estimate cuvarianța imparțială a gnμ(X):VAr(gnμ(X))=n−11eu=1∑n(g(Xeu)−gnμ(X))2.
Exemplu simplu
Cum va afecta incertitudinea privind prețul unitar, vânzările unitare și costurile variabile? EBITD?

Imagine de Sabrina Jiang © Investopedia 2021
( Vanzari unitati)-(Costuri variabile + Costuri fixe)
Să explicăm incertitudinea în intrări - preț unitar, vânzări unitare și costuri variabile - folosind distribuție triunghiulară, specificată de valorile minime și maxime respective ale intrărilor din masa.
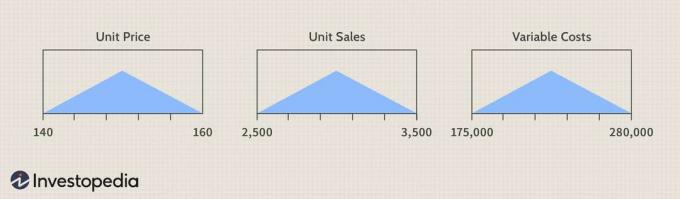
Imagine de Sabrina Jiang © Investopedia 2021
Copright.
Diagrama de sensibilitate
A sensibilitate graficul poate fi foarte util atunci când vine vorba de analiza efectului intrărilor asupra ieșirii. Ceea ce spune este că vânzările unitare reprezintă 62% din varianța EBITD simulată, costurile variabile pentru 28,6% și prețul unitar pentru 9,4%. Corelația dintre vânzările unitare și EBITD și între prețul unitar și EBITD este pozitivă sau o creștere a vânzărilor unitare sau a prețului unitar va duce la o creștere a EBITD. Costurile variabile și EBITD, pe de altă parte, sunt corelate negativ, iar prin scăderea costurilor variabile vom crește EBITD.
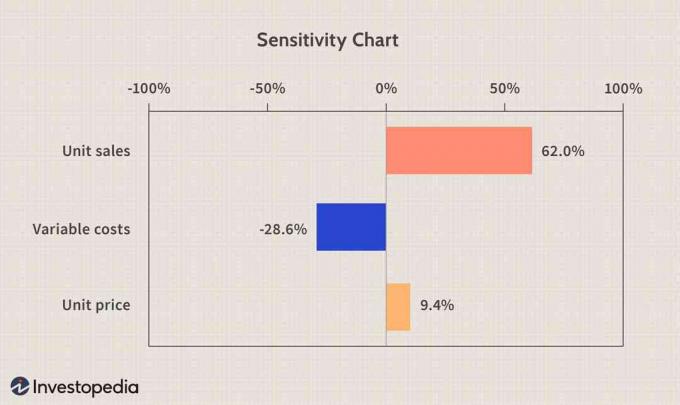
Imagine de Sabrina Jiang © Investopedia 2021
Rețineți că definirea incertitudinii unei valori de intrare printr-o distribuție de probabilitate care nu corespunde cu cea reală și prelevarea de probe din aceasta va da rezultate incorecte. În plus, presupunerea că variabilele de intrare sunt independente s-ar putea să nu fie valabilă. Rezultatele înșelătoare pot proveni din intrări care se exclud reciproc sau dacă se găsește o corelație semnificativă între două sau mai multe distribuții de intrare.
Linia de fund
Tehnica MCS este simplă și flexibilă. Nu poate elimina incertitudinea și riscul, dar le poate face mai ușor de înțeles prin atribuirea caracteristicilor probabilistice la intrările și ieșirile unui model. Poate fi foarte util pentru determinarea diferitelor riscuri și factori care afectează variabilele prognozate și, prin urmare, poate duce la predicții mai precise. De asemenea, rețineți că numărul de încercări nu ar trebui să fie prea mic, deoarece s-ar putea să nu fie suficient pentru a simula modelul, provocând gruparea valorilor.
