Intelligenter wetten mit der Monte-Carlo-Simulation
Im Finanzbereich ist die Schätzung der zukünftiger Wert von Zahlen oder Beträgen aufgrund der Vielzahl möglicher Ergebnisse. Monte-Carlo-Simulation (MCS) ist eine Technik, die hilft, die Unsicherheit bei der Schätzung zukünftiger Ergebnisse zu reduzieren. MCS kann auf komplexe, nichtlineare Modelle angewendet oder zur Bewertung der Genauigkeit und Leistung anderer Modelle verwendet werden. Es kann auch in Risikomanagement, Portfoliomanagement, Preisderivaten, strategischer Planung, Projektplanung, Kostenmodellierung und anderen Bereichen eingesetzt werden.
Definition von MCS
MCS ist eine Technik, die Unsicherheiten in Eingabevariablen eines Modells in Wahrscheinlichkeitsverteilungen umwandelt. Durch Kombinieren der Verteilungen und zufällige Auswahl von Werten daraus wird das simulierte Modell viele Male neu berechnet und die Wahrscheinlichkeit der Ausgabe ermittelt.
Grundlegende Eigenschaften
- MCS ermöglicht die gleichzeitige Verwendung mehrerer Eingaben, um die Wahrscheinlichkeitsverteilung einer oder mehrerer Ausgaben zu erstellen.
- Den Eingaben des Modells können verschiedene Arten von Wahrscheinlichkeitsverteilungen zugeordnet werden. Wenn die Verteilung unbekannt ist, kann diejenige ausgewählt werden, die die beste Anpassung darstellt.
- Die Verwendung von Zufallszahlen charakterisiert MCS als a stochastisch Methode. Die Zufallszahlen müssen unabhängig sein; Nein Korrelation sollte zwischen ihnen bestehen.
- MCS generiert die Ausgabe als Bereich statt als Festwert und zeigt an, wie wahrscheinlich der Ausgabewert im Bereich auftritt.
Einige häufig verwendete Wahrscheinlichkeitsverteilungen in MCS
Normal/Gaußsche Verteilung: Kontinuierliche Verteilung in Situationen, in denen der Mittelwert und der Standardabweichung gegeben und der Mittelwert stellt den wahrscheinlichsten Wert der Variablen dar. Sie ist symmetrisch um den Mittelwert und nicht beschränkt.
Lognormalverteilung: Stetige Verteilung angegeben durch Mittelwert und Standardabweichung. Dies ist für eine Variable im Bereich von Null bis Unendlich geeignet, wobei positiv Schiefe und mit einem normalverteilten natürlichen Logarithmus.
Dreiecksverteilung: Kontinuierliche Verteilung mit festen Minimal- und Maximalwerten. Er wird durch die Minimal- und Maximalwerte begrenzt und kann entweder symmetrisch (wahrscheinlichster Wert = Mittelwert = Median) oder asymmetrisch sein.
Gleichmäßige Verteilung: Stetige Verteilung begrenzt durch bekannte Minimal- und Maximalwerte. Im Gegensatz zur Dreiecksverteilung ist die Eintrittswahrscheinlichkeit der Werte zwischen Minimum und Maximum gleich.
Exponentialverteilung: Kontinuierliche Verteilung, die verwendet wird, um die Zeit zwischen unabhängigen Ereignissen zu veranschaulichen, vorausgesetzt, die Häufigkeit der Ereignisse ist bekannt.
Die Mathematik hinter MCS
Betrachten wir eine reellwertige Funktion g (X) mit Wahrscheinlichkeitshäufigkeitsfunktion P(x) (wenn X diskret ist) oder Wahrscheinlichkeitsdichtefunktion f (x) (wenn X stetig ist). Dann können wir den Erwartungswert von g (X) diskret bzw. stetig definieren:
E(g(x))=−∞∑+∞g(x)P(x), wo P(x)>0 und−∞∑+∞P(x)=1E(g(x))=∫−∞+∞g(x)F(x)Dx, wo F(x)>0 und ∫−∞+∞F(x)Dx=1Als nächstes mach n zufällige Zeichnungen von x(x1,…,xn), namensProbeläufe oder Simulationsläufe, berechnen g(x1),…,g(xn)und finde den Mittelwert von g(x) der Probe:
gnμ(x)=n1ich=1∑ng(xich), was die endgültige simulierteWert von E(g(x)).Deswegen gnμ(x)=n1ich=1∑ng(x) wird das Monte CarloSchätzer von E(g(x)).Wie n→∞,gnμ(x)→E(g(x)),damit sind wir jetzt in der lageberechne die Streuung um den geschätzten Mittelwert mitdie unverzerrte Varianz von gnμ(x):VeinR(gnμ(x))=n−11ich=1∑n(g(xich)−gnμ(x))2.
Einfaches Beispiel
Wie wird sich die Unsicherheit bei Stückpreis, Stückverkauf und variablen Kosten auf die EBITD?

Bild von Sabrina Jiang © Investopedia 2021
( Stückzahlen)-(Variable Kosten + Fixkosten)
Erklären wir die Unsicherheit bei den Inputs – Stückpreis, Stückverkauf und variable Kosten – mit Dreiecksverteilung, angegeben durch die jeweiligen Minimal- und Maximalwerte der Eingaben aus Die Tabelle.
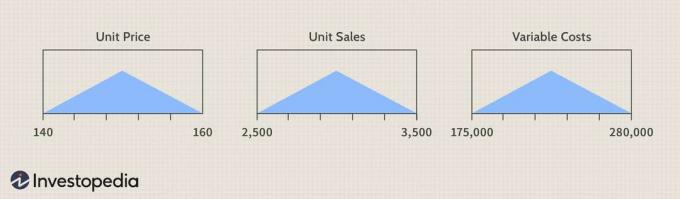
Bild von Sabrina Jiang © Investopedia 2021
Urheberrecht.
Empfindlichkeitstabelle
EIN Empfindlichkeit Diagramm kann sehr nützlich sein, wenn es darum geht, die Auswirkungen der Eingaben auf die Ausgabe zu analysieren. Es heißt, dass der Stückverkauf 62 % der Varianz des simulierten EBITD ausmacht, die variablen Kosten 28,6 % und der Stückpreis 9,4 %. Die Korrelation zwischen Absatz und EBITD sowie zwischen Stückpreis und EBITD ist positiv bzw. ein Anstieg des Absatzes bzw. des Stückpreises führt zu einem Anstieg des EBITD. Variable Kosten und EBITD hingegen sind negativ korreliert, und durch Senkung der variablen Kosten werden wir das EBITD steigern.
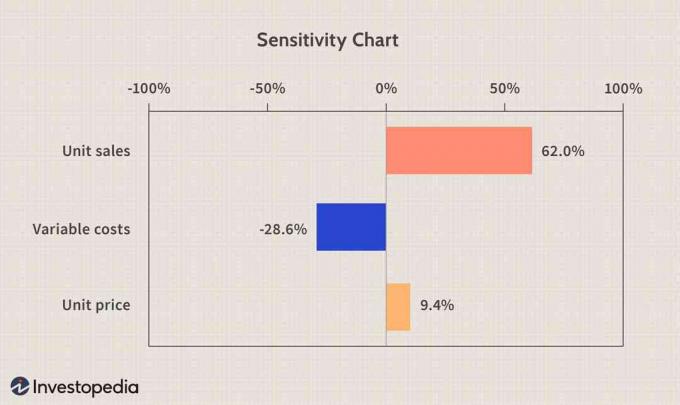
Bild von Sabrina Jiang © Investopedia 2021
Beachten Sie, dass das Definieren der Unsicherheit eines Eingabewerts durch eine Wahrscheinlichkeitsverteilung, die nicht der realen Verteilung entspricht, und die Stichprobenziehung daraus falsche Ergebnisse liefert. Darüber hinaus ist die Annahme, dass die Eingabevariablen unabhängig sind, möglicherweise nicht gültig. Irreführende Ergebnisse können von Eingaben stammen, die sich gegenseitig ausschließen, oder wenn eine signifikante Korrelation zwischen zwei oder mehr Eingabeverteilungen gefunden wird.
Die Quintessenz
Die MCS-Technik ist unkompliziert und flexibel. Es kann Unsicherheit und Risiken nicht auslöschen, aber es kann sie leichter verständlich machen, indem es den Inputs und Outputs eines Modells probabilistische Eigenschaften zuschreibt. Es kann sehr nützlich sein, um verschiedene Risiken und Faktoren zu bestimmen, die sich auf prognostizierte Variablen auswirken, und kann daher zu genaueren Vorhersagen führen. Beachten Sie auch, dass die Anzahl der Versuche nicht zu klein sein sollte, da sie möglicherweise nicht ausreicht, um das Modell zu simulieren, wodurch eine Clusterbildung von Werten auftritt.
