Lieciet gudrāk, izmantojot Montekarlo simulāciju
Finanšu jomā ir diezgan daudz nenoteiktības un riska, kas saistīts ar to novērtēšanu nākotnes vērtība daudzu iespējamo rezultātu dēļ. Montekarlo simulācija (MCS) ir viena metode, kas palīdz mazināt nenoteiktību, kas saistīta ar nākotnes rezultātu novērtēšanu. MCS var piemērot sarežģītiem, nelineāriem modeļiem vai izmantot, lai novērtētu citu modeļu precizitāti un veiktspēju. To var īstenot arī riska pārvaldībā, portfeļa pārvaldībā, atvasināto finanšu instrumentu cenu noteikšanā, stratēģiskajā plānošanā, projektu plānošanā, izmaksu modelēšanā un citās jomās.
MCS definīcija
MCS ir metode, kas pārveido modeļa ievades mainīgo nenoteiktību varbūtības sadalījumā. Apvienojot sadalījumus un nejauši izvēloties no tiem vērtības, tas daudzas reizes pārrēķina simulēto modeli un parāda iznākuma varbūtību.
Pamatīpašības
- MCS ļauj vienlaikus izmantot vairākas ievades, lai izveidotu vienas vai vairāku izeju varbūtības sadalījumu.
- Modeļa ievadiem var piešķirt dažādus varbūtības sadalījumu veidus. Ja izplatīšana nav zināma, var izvēlēties to, kas vislabāk atbilst.
- Nejaušu skaitļu izmantošana raksturo MCS kā a stohastisks metodi. Nejaušiem skaitļiem jābūt neatkarīgiem; Nē korelācija starp tām vajadzētu pastāvēt.
- MCS ģenerē izvadi kā diapazonu, nevis fiksētu vērtību un parāda, cik liela ir iespējamība, ka izvades vērtība notiks diapazonā.
Daži bieži lietoti varbūtību sadalījumi MCS
Normāls/Gausa sadalījums: Nepārtraukta izplatīšana, ko piemēro situācijās, kad vidējais un standarta novirze ir norādīti, un vidējais rādītājs ir visticamākā mainīgā vērtība. Tas ir simetrisks ap vidējo un nav ierobežots.
Lognormālais sadalījums: Nepārtraukts sadalījums, ko nosaka vidējā un standarta novirze. Tas ir piemērots mainīgajam, sākot no nulles līdz bezgalībai, ar pozitīvu šķība un ar normāli sadalītu dabisko logaritmu.
Trīsstūrveida sadalījums: Nepārtraukta izplatīšana ar fiksētām minimālajām un maksimālajām vērtībām. To ierobežo minimālās un maksimālās vērtības, un tas var būt vai nu simetrisks (visticamākā vērtība = vidējais = mediāna), vai asimetrisks.
Vienveidīgs sadalījums: Nepārtraukta izplatīšana, ko ierobežo zināmās minimālās un maksimālās vērtības. Atšķirībā no trīsstūrveida sadalījuma, varbūtību parādīties starp minimālo un maksimālo vērtību ir vienāda.
Eksponenciālais sadalījums: Nepārtraukta izplatīšana, ko izmanto, lai ilustrētu laiku starp neatkarīgiem notikumiem, ja ir zināms notikumu ātrums.
Matemātika aiz MCS
Apsveriet, ka mums ir reāli novērtēta funkcija g (X) ar varbūtības frekvences funkciju P (x) (ja X ir diskrēta) vai varbūtības blīvuma funkcija f (x) (ja X ir nepārtraukta). Tad mēs varam definēt paredzamo g (X) vērtību attiecīgi diskrētā un nepārtrauktā izteiksmē:
E(g(X))=−∞∑+∞g(x)Lpp(x), kur Lpp(x)>0 un−∞∑+∞Lpp(x)=1E(g(X))=∫−∞+∞g(x)f(x)dx, kur f(x)>0 un ∫−∞+∞f(x)dx=1Tālāk izveidojiet n izlases zīmējumi no X(x1,…,xn), zvanījaizmēģinājuma vai simulācijas braucieni, aprēķiniet g(x1),…,g(xn)un atrast vidējo g(x) no parauga:
gnμ(x)=n1i=1∑ng(xi), kas attēlo simulēto galīgovērtība E(g(X)).Tāpēc gnμ(X)=n1i=1∑ng(X) būs Montekarloaprēķinātājs E(g(X)).Kā n→∞,gnμ(X)→E(g(X)),tāpēc mēs tagad varamaprēķiniet dispersiju ap paredzamo vidējo arobjektīvā dispersija gnμ(X):Var(gnμ(X))=n−11i=1∑n(g(xi)−gnμ(x))2.
Vienkāršs piemērs
Kā ietekmēs vienības cenas, vienības pārdošanas un mainīgo izmaksu nenoteiktība EBITD?

Sabrina Jiang attēls © Investopedia 2021
(Vienības pārdošana)-(Mainīgas izmaksas + Fiksētas izmaksas)
Paskaidrosim nenoteiktību, ko rada izejvielas - vienības cena, vienības pārdošana un mainīgās izmaksas trīsstūrveida sadalījums, ko nosaka attiecīgās minimālās un maksimālās ieejas vērtības no galds.
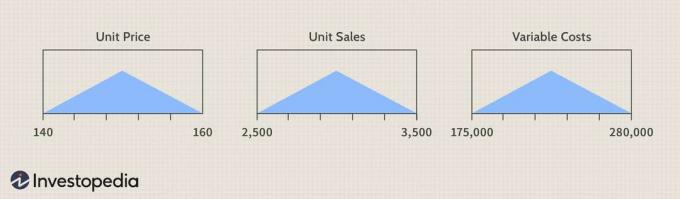
Sabrina Jiang attēls © Investopedia 2021
Copright.
Jutīguma tabula
A jutīgums diagramma var būt ļoti noderīga, analizējot ievades ietekmi uz izvadi. Tas saka, ka vienības pārdošana veido 62%no simulētās EBITD dispersijas, mainīgās izmaksas - 28,6%un vienības cena - 9,4%. Korelācija starp vienības pārdošanu un EBITD un vienības cenu un EBITD ir pozitīva, vai vienības pārdošanas vai vienības cenas pieaugums izraisīs EBITD pieaugumu. Savukārt mainīgās izmaksas un EBITD ir negatīvi saistītas, un, samazinot mainīgās izmaksas, mēs palielināsim EBITD.
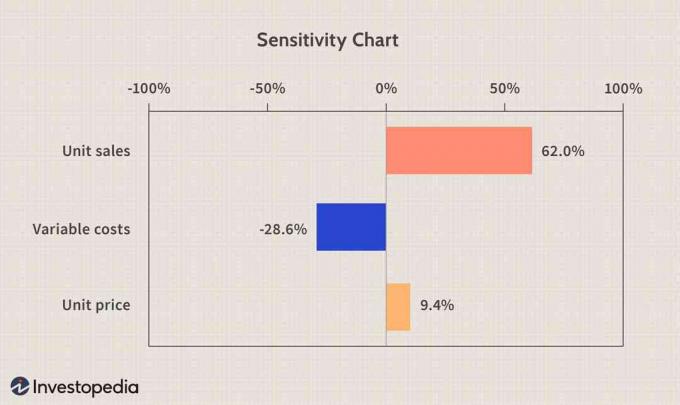
Sabrina Jiang attēls © Investopedia 2021
Uzmanieties, ka ievades vērtības nenoteiktības definēšana ar varbūtības sadalījumu, kas neatbilst reālajam, un paraugu ņemšana no tās dos nepareizus rezultātus. Turklāt pieņēmums, ka ievades mainīgie ir neatkarīgi, var nebūt pamatots. Maldinoši rezultāti var rasties, ievadot informāciju, kas ir savstarpēji izslēdzoši, vai ja tiek konstatēta būtiska korelācija starp diviem vai vairākiem ievades sadalījumiem.
Bottom Line
MCS tehnika ir vienkārša un elastīga. Tas nevar iznīcināt nenoteiktību un risku, bet var atvieglot to izpratni, modeļa ievadei un rezultātam piešķirot varbūtības pazīmes. Tas var būt ļoti noderīgi, lai noteiktu dažādus riskus un faktorus, kas ietekmē prognozējamos mainīgos lielumus, un tāpēc tas var radīt precīzākas prognozes. Ņemiet vērā arī to, ka izmēģinājumu skaitam nevajadzētu būt pārāk mazam, jo ar to var nepietikt, lai modelētu modeli, izraisot vērtību klasterizāciju.
