Untersuchung des exponentiell gewichteten gleitenden Durchschnitts

Volatilität ist das häufigste Risikomaß, aber es gibt verschiedene Varianten. In einem früheren Artikel haben wir gezeigt, wie man einfach berechnet historische Volatilität. In diesem Artikel werden wir die einfache Volatilität verbessern und den exponentiell gewichteten gleitenden Durchschnitt (EWMA) diskutieren.

Historisch vs. Implizite Volatilität

Lassen Sie uns diese Metrik zunächst etwas in die richtige Perspektive rücken. Es gibt zwei breite Ansätze: historische und implizite (oder implizite) Volatilität. Der historische Ansatz geht davon aus, dass die Vergangenheit ein Prolog ist; Wir messen die Geschichte in der Hoffnung, dass sie vorhersagbar ist. Implizite Volatilität hingegen ignoriert die Geschichte; es löst nach der durch die Marktpreise implizierten Volatilität auf. Sie hofft, dass der Markt es am besten weiß und dass die Marktpreis enthält, wenn auch implizit, a Konsensschätzung der Volatilität.

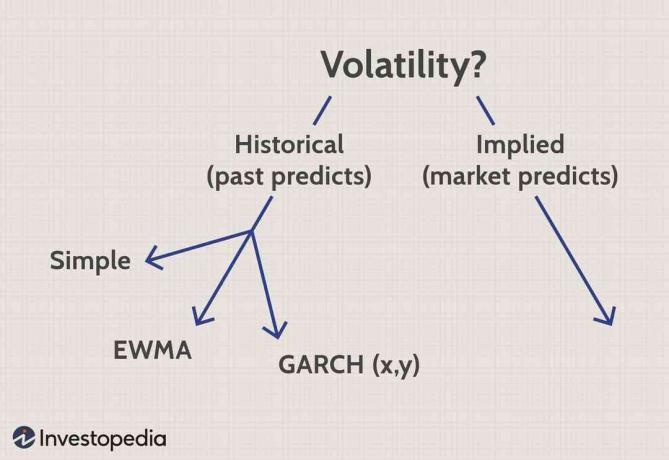
Wenn wir uns nur auf die drei historischen Ansätze (links oben) konzentrieren, haben sie zwei Schritte gemeinsam:

1. Berechnen Sie die Reihe der periodischen Renditen
2. Gewichtungsschema anwenden

Zuerst berechnen wir die periodische Rendite. Das ist in der Regel eine Reihe von täglichen Renditen, wobei jede Rendite in kontinuierlich zusammengesetzten Begriffen ausgedrückt wird. Für jeden Tag nehmen wir den natürlichen Logarithmus des Verhältnisses der Aktienkurse (d. h. den heutigen Kurs dividiert durch den gestrigen Kurs usw.).

​duich​=lnSich−1​Sich​​wo:duich​=Rückkehr am Tag ichSich​=Aktienkurs am Tag ichSich−1​=Aktienkurs am Vortag ich​

Dies führt zu einer Reihe von täglichen Renditen, von u_ich für dich_{Ich bin}, je nachdem wie viele Tage (m = Tage) wir messen.

Damit kommen wir zum zweiten Schritt: Hier unterscheiden sich die drei Ansätze. Im vorherigen Artikel haben wir gezeigt, dass unter ein paar akzeptablen Vereinfachungen die einfachen Abweichung ist der Durchschnitt der quadrierten Renditen:

​Abweichung=σn2​=m1​ich=1∑m​dun−12​wo:m=Anzahl der gemessenen Tagen=Tag ichdu=Differenz der Rendite von der durchschnittlichen Rendite​

Beachten Sie, dass dies jede der periodischen Rückgaben summiert und dann diese Summe durch die Anzahl der Tage oder Beobachtungen (m) dividiert. Es ist also wirklich nur ein Durchschnitt der quadrierten periodischen Renditen. Anders ausgedrückt, jede quadrierte Rendite wird gleich gewichtet. Also wenn Alpha (a) ein Gewichtungsfaktor ist (genauer gesagt a = 1/m), dann sieht eine einfache Varianz etwa so aus:

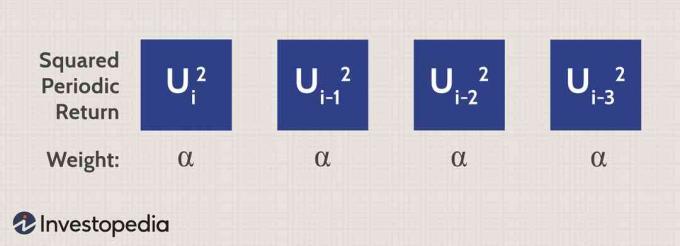
Die EWMA verbessert die einfache Varianz
Die Schwäche dieses Ansatzes besteht darin, dass alle Renditen das gleiche Gewicht haben. Die gestrige (jüngste) Rendite hat keinen größeren Einfluss auf die Varianz als die Rendite des Vormonats. Dieses Problem wird durch die Verwendung des exponentiell gewichteten gleitenden Durchschnittes (EWMA) behoben, bei dem neuere Renditen ein größeres Gewicht auf die Varianz haben.

Der exponentiell gewichtete gleitende Durchschnitt (EWMA) führt ein Lambda, der Glättungsparameter genannt wird. Lambda muss kleiner als eins sein. Unter dieser Bedingung wird jede quadrierte Rendite anstelle von gleichen Gewichten mit a. gewichtet Multiplikator wie folgt:

Zum Beispiel RiskMetrics^TM_, ein finanzielles Risiko Verwaltungsgesellschaft, verwendet tendenziell ein Lambda von 0,94 oder 94 %.In diesem Fall wird die erste (jüngste) quadrierte periodische Rendite mit (1-0.94)(.94) gewichtet.⁰ = 6%. Die nächste quadrierte Rendite ist einfach ein Lambda-Vielfaches der vorherigen Gewichtung; in diesem Fall 6% multipliziert mit 94% = 5,64%. Und das Gewicht des dritten Vortages entspricht (1-0,94)(0,94)² = 5.30%.

Das ist die Bedeutung von "exponentiell" in EWMA: Jedes Gewicht ist ein konstanter Multiplikator (dh Lambda, das kleiner als eins sein muss) des Gewichts des Vortages. Dies stellt eine Varianz sicher, die gegenüber neueren Daten gewichtet oder verzerrt ist. Der Unterschied zwischen einfacher Volatilität und EWMA für Google wird unten gezeigt.

Einfache Volatilität wiegt effektiv jede einzelne periodische Rendite mit 0,196%, wie in Spalte O gezeigt (wir hatten zwei Jahre tägliche Aktienkursdaten. Das sind 509 Tagesrenditen und 1/509 = 0,196%). Beachten Sie jedoch, dass Spalte P eine Gewichtung von 6%, dann 5,64%, dann 5,3% usw. zuweist. Das ist der einzige Unterschied zwischen einfacher Varianz und EWMA.

Denken Sie daran: Nachdem wir die gesamte Reihe (in Spalte Q) summiert haben, haben wir die Varianz, die das Quadrat der Standardabweichung. Wenn wir Volatilität wollen, müssen wir daran denken, die Quadratwurzel dieser Varianz zu ziehen.

Was ist der Unterschied in der täglichen Volatilität zwischen der Varianz und dem EWMA im Fall von Google? Es ist signifikant: Die einfache Varianz lieferte uns eine tägliche Volatilität von 2,4%, aber der EWMA gab eine tägliche Volatilität von nur 1,4% an (siehe Tabelle für Details). Anscheinend hat sich die Volatilität von Google in letzter Zeit beruhigt; daher kann eine einfache Varianz künstlich hoch sein.

Die heutige Varianz ist eine Funktion der Varianz des Vortages

Sie werden feststellen, dass wir eine lange Reihe exponentiell abnehmender Gewichtungen berechnen mussten. Wir werden hier nicht nachrechnen, aber eine der besten Eigenschaften der EWMA ist, dass sich die gesamte Serie praktischerweise auf eine rekursive Formel reduziert:

​σn2​(EWMA)=λσn−12​+(1−λ)dun−12​wo:EWMA=Exponentiell gewichteter gleitender Durchschnittσn2​=Abweichung heuteλ=Gewichtungsgradσn−12​=Abweichung gesterndun−12​=Quadratische Rückkehr gestern​

Rekursiv bedeutet, dass die heutige Varianz auf die Varianz des Vortages verweist (d. h. eine Funktion davon ist). Sie finden diese Formel auch in der Kalkulationstabelle und sie liefert genau das gleiche Ergebnis wie die handschriftliche Berechnung! Es besagt: Die heutige Varianz (unter EWMA) ist gleich der gestrigen Varianz (gewichtet mit Lambda) plus der gestrigen quadrierten Rendite (gewichtet mit eins minus Lambda). Beachten Sie, wie wir nur zwei Terme addieren: die gewichtete Varianz von gestern und die gewichtete quadrierte Rendite von gestern.

Trotzdem ist Lambda unser Glättungsparameter. Ein höheres Lambda (z. B. wie die 94% von RiskMetric) zeigt einen langsameren Zerfall in der Reihe an – in relativen Begriffe, wir werden mehr Datenpunkte in der Serie haben und sie werden mehr "abfallen" langsam. Reduzieren wir hingegen das Lambda, zeigen wir einen höheren Zerfall an: Die Gewichte fallen schneller ab und als direkte Folge des schnellen Zerfalls werden weniger Datenpunkte verwendet. (In der Tabelle ist Lambda eine Eingabe, sodass Sie mit seiner Empfindlichkeit experimentieren können).

Zusammenfassung

Volatilität ist die momentane Standardabweichung einer Aktie und die häufigste Risikokennzahl. Es ist auch die Quadratwurzel der Varianz. Wir können die Varianz historisch oder implizit (implizite Volatilität) messen. Bei der historischen Messung ist die einfachste Methode eine einfache Varianz. Die Schwäche bei der einfachen Varianz besteht jedoch darin, dass alle Renditen das gleiche Gewicht erhalten. Wir stehen also vor einem klassischen Kompromiss: Wir wollen immer mehr Daten, aber je mehr Daten wir haben, desto mehr wird unsere Berechnung durch entfernte (weniger relevante) Daten verwässert. Der exponentiell gewichtete gleitende Durchschnitt (EWMA) verbessert die einfache Varianz, indem er den periodischen Renditen Gewichte zuweist. Auf diese Weise können wir sowohl eine große Stichprobengröße verwenden, als auch jüngeren Renditen mehr Gewicht geben.