Staňte sa múdrejšími so simuláciou Monte Carlo
Vo financiách je s odhadom odhadu spojená značná miera neistoty a rizika budúca hodnota čísiel alebo súm vzhľadom na širokú škálu potenciálnych výsledkov. Simulácia Monte Carlo (MCS) je jednou z techník, ktoré pomáhajú znižovať neistotu pri odhadovaní budúcich výsledkov. MCS je možné použiť na komplexné nelineárne modely alebo ho použiť na vyhodnotenie presnosti a výkonu iných modelov. Je možné ho implementovať aj do riadenia rizík, správy portfólia, cenových derivátov, strategického plánovania, projektového plánovania, nákladového modelovania a ďalších oblastí.
Definícia MCS
MCS je technika, ktorá prevádza neistoty vo vstupných premenných modelu na rozdelenie pravdepodobnosti. Kombináciou distribúcií a náhodným výberom hodnôt z nich mnohokrát prepočíta simulovaný model a odhalí pravdepodobnosť výstupu.
Základné vlastnosti
- MCS umožňuje použiť niekoľko vstupov súčasne na vytvorenie rozdelenia pravdepodobnosti jedného alebo viacerých výstupov.
- Vstupom modelu je možné priradiť rôzne typy rozdelení pravdepodobnosti. Ak je distribúcia neznáma, môže byť zvolené to, ktoré najlepšie vyhovuje.
- Použitie náhodných čísel charakterizuje MCS ako a stochastický metóda. Náhodné čísla musia byť nezávislé; č korelácia by mala existovať medzi nimi.
- MCS generuje výstup ako rozsah namiesto pevnej hodnoty a ukazuje, ako pravdepodobne sa výstupná hodnota v rozsahu vyskytne.
Niektoré často používané distribúcie pravdepodobnosti v MCS
Normálna/Gaussova distribúcia: Kontinuálna distribúcia aplikovaná v situáciách, kde priemer a štandardná odchýlka sú dané a priemer predstavuje najpravdepodobnejšiu hodnotu premennej. Je symetrický okolo priemeru a nie je ohraničený.
Lognormálna distribúcia: Spojité rozdelenie špecifikované priemerom a štandardnou odchýlkou. To je vhodné pre premennú v rozsahu od nuly do nekonečna, s kladnou hodnotou šikmosť a s normálne rozloženým prírodným logaritmom.
Trojuholníková distribúcia: Nepretržitá distribúcia s pevnými minimálnymi a maximálnymi hodnotami. Je ohraničená minimálnymi a maximálnymi hodnotami a môže byť symetrická (najpravdepodobnejšia hodnota = priemer = medián) alebo asymetrická.
Rovnomerné rozdelenie: Spojitá distribúcia ohraničená známymi minimálnymi a maximálnymi hodnotami. Na rozdiel od trojuholníkového rozloženia je pravdepodobnosť výskytu hodnôt medzi minimom a maximom rovnaká.
Exponenciálna distribúcia: Kontinuálna distribúcia používaná na ilustráciu času medzi nezávislými výskytmi za predpokladu, že je známa miera výskytu.
Matematika za MCS
Uvažujme, že máme funkciu s reálnou hodnotou g (X) s frekvenčnou funkciou pravdepodobnosti P (x) (ak je X diskrétne) alebo funkciu hustoty pravdepodobnosti f (x) (ak je X spojitá). Potom môžeme definovanú očakávanú hodnotu g (X) definovať diskrétne a spojito:
E(g(X))=−∞∑+∞g(X)P(X), kde P(X)>0 a−∞∑+∞P(X)=1E(g(X))=∫−∞+∞g(X)f(X)dX, kde f(X)>0 a ∫−∞+∞f(X)dX=1Ďalej urobte n náhodné kresby z X(X1,…,Xn), zavolalskúšobné alebo simulačné jazdy, vypočítajte g(X1),…,g(Xn)a nájsť priemer g(X) vzorky:
gnμ(X)=n1i=1∑ng(Xi), ktorý predstavuje konečnú simulovanúhodnota E(g(X)).Preto gnμ(X)=n1i=1∑ng(X) bude Monte Carloodhadca z E(g(X)).Ako n→∞,gnμ(X)→E(g(X)),tak sme teraz schopnívypočítajte disperziu okolo odhadovaného priemeru pomocounezaujatý rozptyl gnμ(X):Var(gnμ(X))=n−11i=1∑n(g(Xi)−gnμ(X))2.
Jednoduchý príklad
Ako ovplyvní neistota v jednotkovej cene, jednotkových tržbách a variabilných nákladoch EBITD?

Obrázok Sabriny Jiangovej © Investopedia 2021
(Jednotkový predaj)-(Variabilné náklady + Nemenné ceny)
Vysvetlíme neistotu vo vstupoch - jednotková cena, jednotkové tržby a variabilné náklady - pomocou trojuholníkové rozdelenie, určené príslušnými minimálnymi a maximálnymi hodnotami vstupov z stôl.
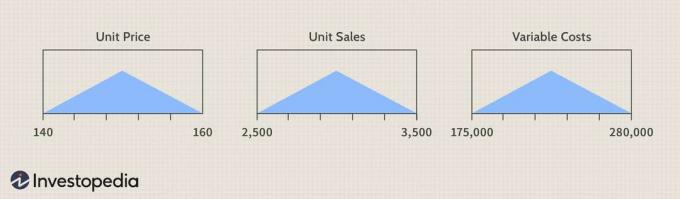
Obrázok Sabriny Jiangovej © Investopedia 2021
Copright.
Tabuľka citlivosti
A citlivosť graf môže byť veľmi užitočný, pokiaľ ide o analýzu účinku vstupov na výstup. Hovorí sa, že jednotkové tržby predstavujú 62%odchýlok v simulovanom EBITD, variabilné náklady 28,6%a jednotková cena 9,4%. Korelácia medzi jednotkovým predajom a EBITD a medzi jednotkovou cenou a EBITD je pozitívna alebo zvýšenie jednotkového predaja alebo jednotkovej ceny povedie k zvýšeniu EBITD. Variabilné náklady a EBITD na druhej strane negatívne korelujú a znížením variabilných nákladov zvýšime EBITD.
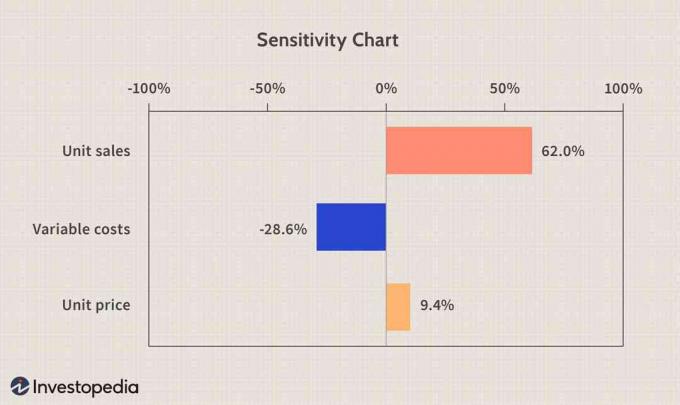
Obrázok Sabriny Jiangovej © Investopedia 2021
Dávajte si pozor na to, že definovanie neistoty vstupnej hodnoty rozdelením pravdepodobnosti, ktoré nezodpovedá skutočnej a výber z nej poskytne nesprávne výsledky. Navyše predpoklad, že vstupné premenné sú nezávislé, nemusí byť platný. Klamlivé výsledky môžu pochádzať zo vstupov, ktoré sa navzájom vylučujú, alebo ak sa zistí významná korelácia medzi dvoma alebo viacerými distribúciami vstupov.
Spodný riadok
Technika MCS je jednoduchá a flexibilná. Nemôže vymazať neistotu a riziko, ale môže ich uľahčiť porozumenie pripisovaním pravdepodobnostných charakteristík vstupom a výstupom modelu. Môže byť veľmi užitočný pri určovaní rôznych rizík a faktorov, ktoré ovplyvňujú predpovedané premenné, a preto môže viesť k presnejším predpovediam. Všimnite si tiež, že počet pokusov by nemal byť príliš malý, pretože nemusí postačovať na simuláciu modelu, čo spôsobuje zoskupovanie hodnôt.
