Obstawiaj mądrzej dzięki symulacji Monte Carlo
W finansach istnieje spora niepewność i ryzyko związane z oszacowaniem przyszła wartość liczb lub kwot ze względu na dużą różnorodność potencjalnych wyników. Symulacja Monte Carlo (MCS) to jedna z technik, która pomaga zmniejszyć niepewność związaną z szacowaniem przyszłych wyników. MCS można zastosować do złożonych, nieliniowych modeli lub wykorzystać do oceny dokładności i wydajności innych modeli. Może być również wdrożony w zarządzaniu ryzykiem, zarządzaniu portfelem, instrumentach pochodnych cenowych, planowaniu strategicznym, planowaniu projektów, modelowaniu kosztów i innych dziedzinach.
Definicja MCS
MCS to technika, która przekształca niepewności zmiennych wejściowych modelu na rozkłady prawdopodobieństwa. Łącząc rozkłady i losowo wybierając z nich wartości, wielokrotnie przelicza symulowany model i wydobywa prawdopodobieństwo wyjścia.
Podstawowe cechy
- MCS pozwala na jednoczesne użycie kilku danych wejściowych w celu stworzenia rozkładu prawdopodobieństwa jednego lub większej liczby danych wyjściowych.
- Wejściom modelu można przypisać różne typy rozkładów prawdopodobieństwa. Gdy rozkład jest nieznany, można wybrać ten, który reprezentuje najlepsze dopasowanie.
- Użycie liczb losowych charakteryzuje MCS jako a stochastyczny metoda. Liczby losowe muszą być niezależne; nie korelacja powinno istnieć między nimi.
- MCS generuje dane wyjściowe jako zakres zamiast wartości stałej i pokazuje prawdopodobieństwo wystąpienia wartości wyjściowej w zakresie.
Niektóre często używane rozkłady prawdopodobieństwa w MCS
Rozkład normalny/Gaussowski: Rozkład ciągły stosowany w sytuacjach, gdy średnia i odchylenie standardowe są podane, a średnia reprezentuje najbardziej prawdopodobną wartość zmiennej. Jest symetryczny wokół średniej i nie jest ograniczony.
Rozkład logarytmiczny: Rozkład ciągły określony przez średnią i odchylenie standardowe. Jest to odpowiednie dla zmiennej od zera do nieskończoności, z dodatnim skośność oraz z logarytmem naturalnym o rozkładzie normalnym.
Rozkład trójkątny: Rozkład ciągły ze stałymi wartościami minimalnymi i maksymalnymi. Jest ograniczony wartościami minimalnymi i maksymalnymi i może być symetryczny (wartość najbardziej prawdopodobna = średnia = mediana) lub asymetryczny.
Dystrybucja równomierna: Rozkład ciągły ograniczony znanymi wartościami minimalnymi i maksymalnymi. W przeciwieństwie do rozkładu trójkątnego prawdopodobieństwo wystąpienia wartości pomiędzy minimum a maksimum jest takie samo.
Rozkład wykładniczy: Rozkład ciągły używany do zilustrowania czasu między niezależnymi zdarzeniami, pod warunkiem, że znany jest wskaźnik zdarzeń.
Matematyka za MCS
Rozważmy, że mamy funkcję o wartościach rzeczywistych g (X) z funkcją częstości prawdopodobieństwa P(x) (jeśli X jest dyskretne) lub funkcją gęstości prawdopodobieństwa f (x) (jeśli X jest ciągłe). Następnie możemy zdefiniować oczekiwaną wartość g (X) odpowiednio w kategoriach dyskretnych i ciągłych:
mi(g(x))=−∞∑+∞g(x)P(x), gdzie P(x)>0 oraz−∞∑+∞P(x)=1mi(g(x))=∫−∞+∞g(x)F(x)Dx, gdzie F(x)>0 oraz ∫−∞+∞F(x)Dx=1Następnie zrób n losowe rysunki x(x1,…,xn), zwanyprzebiegi próbne lub symulacje, obliczyć g(x1),…,g(xn)i znajdź średnią z g(x) próbki:
gnμ(x)=n1i=1∑ng(xi), który reprezentuje ostateczną symulacjęwartość mi(g(x)).W związku z tym gnμ(x)=n1i=1∑ng(x) będzie Monte Carloestymator mi(g(x)).NS n→∞,gnμ(x)→mi(g(x)),dzięki temu jesteśmy teraz w stanieobliczyć dyspersję wokół oszacowanej średniej zbezstronna wariancja gnμ(x):Var(gnμ(x))=n−11i=1∑n(g(xi)−gnμ(x))2.
Prosty przykład
Jak niepewność ceny jednostkowej, sprzedaży jednostkowej i kosztów zmiennych wpłynie na EBITD?

Zdjęcie autorstwa Sabriny Jiang © Investopedia 2021
( Sprzedaż jednostkowa)-(Koszty zmienne + Koszty stałe)
Wyjaśnijmy niepewność danych wejściowych — cenę jednostkową, sprzedaż jednostkową i koszty zmienne — za pomocą rozkład trójkątny, określony przez odpowiednie minimalne i maksymalne wartości wejść z stół.
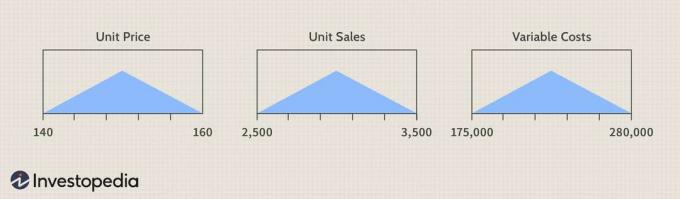
Zdjęcie autorstwa Sabriny Jiang © Investopedia 2021
Prawo autorskie.
Wykres czułości
A wrażliwość wykres może być bardzo przydatny, jeśli chodzi o analizę wpływu danych wejściowych na wynik. Mówi się, że sprzedaż jednostkowa odpowiada za 62% wariancji symulowanego EBITD, koszty zmienne za 28,6%, a cena jednostkowa za 9,4%. Korelacja pomiędzy sprzedażą jednostkową a EBITD oraz pomiędzy ceną jednostkową a EBITD jest dodatnia lub wzrost sprzedaży jednostkowej lub ceny jednostkowej doprowadzi do wzrostu EBITD. Natomiast koszty zmienne i EBITD są ujemnie skorelowane, a zmniejszając koszty zmienne zwiększymy EBITD.
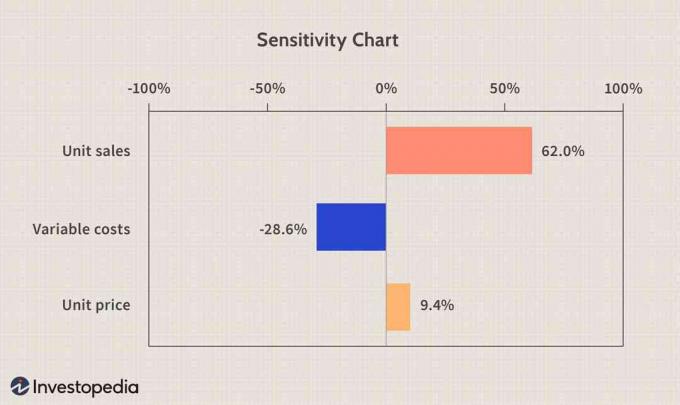
Zdjęcie autorstwa Sabriny Jiang © Investopedia 2021
Należy pamiętać, że definiowanie niepewności wartości wejściowej przez rozkład prawdopodobieństwa, który nie odpowiada rzeczywistemu i pobieranie z niego próbek, da błędne wyniki. Ponadto założenie, że zmienne wejściowe są niezależne, może nie być prawidłowe. Wprowadzające w błąd wyniki mogą pochodzić z danych wejściowych, które wzajemnie się wykluczają lub jeśli zostanie stwierdzona znacząca korelacja między dwoma lub większą liczbą rozkładów danych wejściowych.
Dolna linia
Technika MCS jest prosta i elastyczna. Nie może wyeliminować niepewności i ryzyka, ale może ułatwić ich zrozumienie poprzez przypisanie probabilistycznych cech wejściowych i wyjściowych modelu. Może być bardzo przydatny do określania różnych ryzyk i czynników, które wpływają na prognozowane zmienne, a zatem może prowadzić do dokładniejszych prognoz. Należy również zauważyć, że liczba prób nie powinna być zbyt mała, ponieważ symulacja modelu może być niewystarczająca, powodując grupowanie wartości.
